题目:在一个n位的正整数A[1…n]中删除其中任意k(k≤n)个数字后,剩下的数字按原次序组成一个新的正整数。对于给定的n位正整数A和k,设计一个贪心算法,使得剩下的数字组成的新数最小。
如:A=278693,k=4时最小新数为23,k=3时为263
刚刚证明出来贪心选择性质,先写下,之后再慢慢补充全部思路。
贪心选择策略
从高位向低位进行搜索:
- 如果A[1…n]是一条递增序列,那么就删除最后一个数;
- 如果A[1…n]含有严格递减子序列,那么就删除第一个严格递减子序列的首字符。
贪心选择性质证明
假设A中有n个元素,将A中的每个元素进行编号为$a_x(1\leq x\leq n)$:
$$
A=[a_1,a_2,…,a_{n-1},a_n]
$$
- 如果A[1…n]是一条递增序列,那么就删除最后一个数;
记原本A所代表的数值为$T_A$,则有:
$$
T_A=a_1 \times 10^{n-1}+a_2\times10^{n-2}+…+a_{n-1}\times10+a_n
$$
记删除最后一个数后,A变为A’,A’所代表的数值为$T_{A’}$,则有:
$$
T_{A’}=a_1\times10^{n-2}+a_2 \times 10^{n-3}+…+a_{n-2} \times 10+a_{n-1}
$$
如果不删除最后一个数,而是删除另一个数$a_q(1\leq q< n)$,此时A变为A’’,A’’所代表的数值为$T_{A’’}$,则有:
$$
T_{A’’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_{q-1} \times 10^{n-q}+a_{q+1} \times 10^{n-q-1}+…+a_{n-1} \times 10+a_n
$$
用作差法来比较$T_{A’}$和$T_{A’’}$的大小:
$$
T_{A’}-T_{A’’}=(a_q-a_{q+1}) \times 10^{n-q-1}+(a_{q+1}-a_{q+2}) \times 10^{n-q-2}+…+(a_{n-2}-a_{n-1}) \times 10+(a_{n-1}-a_{n})
$$
由于A是一条递增序列,所以有:
$$
a_{q}\leq a_{q+1},a_{q+1}\leq a_{q+2},…,a_{n-2}\leq a_{n-1},a_{n-1}\leq a_{n}
$$
即:
$$
a_{q}-a_{q+1}\leq 0,a_{q+1}-a_{q+2}\leq 0,…,a_{n-2}-a_{n-1}\leq 0,a_{n-1}-a_{n}\leq 0
$$
所以有$T_{A’}-T_{A’’}\leq 0$,那么$T_{A’}$是A删完一个数后,所组成的最小数值。贪心选择是安全的。
- 如果A[1…n]含有严格递减子序列,那么就删除第一个严格递减子序列的首字符。
(1) 先考虑一种情况,A中只有两段单调子区间,且高位部分是递增子区间,低位部分是递减子区间。那么A中的数就是先上升再下降,像一座山一样。如果删除第一个递减子序列的首字符是安全的,也就是删除山顶的数是安全的。
假设在A中,有3个连在一起的数$a_i,a_j,a_k(1\leq i< j< k\leq n)$,其中$(a_1,a_j)$是递增序列,$(a_j,a_n)$是递减序列。
记原本A所代表的数值为$T_A$,则有:
$$
T_A=a_1 \times 10^{n-1}+a_2 \times 10^{n-2}+…+a_i \times 10^{n-i}+a_j \times 10^{n-j}+a_k \times 10^{n-k}+…+a_{n-1} \times 10+a_n
$$
删除$a_j$后,A变为A’,A’所代表的数值为$T_{A’}$,则有:
$$
T_{A’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_i \times 10^{n-i-1}+a_k \times 10^{n-k}+…+a_{n-1} \times 10+a_{n}
$$
如果不删除$a_j$,而是删除另一个数$a_q$。
a) 当$1\leq q< j$时,此时A变为A’’,A’’所代表的数值为$T_{A’’}$,则有:
$$
T_{A’’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_{q-1} \times 10^{n-q}+a_{q+1} \times 10^{n-q-1}+…+a_j \times 10^{n-j}+…+a_{n-1} \times 10+a_{n}
$$
用作差法来比较$T_{A’}$和$T_{A’’}$的大小:
$$
T_{A’}-T_{A’’}=(a_q-a_{q+1}) \times 10^{n-q-1}+(a_{q+1}-a_{q+2}) \times 10^{n-q-2}+…+(a_{i}-a_{j}) \times 10^{n-j}
$$
由于$(a_1,a_j)$是一条递增序列,所以有:
$$
a_{q}\leq a_{q+1},a_{q+1}\leq a_{q+2},…,a_{i}\leq a_{j}
$$
即:
$$
a_{q}-a_{q+1}\leq 0,a_{q+1}-a_{q+2}\leq 0,…,a_{i}-a_{j}\leq 0
$$
所以有$T_{A’}-T_{A’’}\leq 0$,那么$T_{A’}$是A删完$a_q(1\leq q < j)$后,所组成的最小数值。贪心选择是安全的。
(b) 当$j < q\leq n$时,此时A变为A’’’,A’’’所代表的数值为$T_{A’’’}$,则有:
$$
T_{A’’’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_j \times 10^{n-j-1}+…+a_{q-1} \times 10^{n-q}+a_{q+1} \times 10^{n-q-1}…+a_{n-1} \times 10+a_{n}
$$
用作差法来比较$T_{A’}$和$T_{A’’’}$的大小:
$$
T_{A’}-T_{A’’}=(a_k-a_j) \times 10^{n-k}+…+(a_{q-1}-a_{q-2}) \times 10^{n-q+1}+(a_{q}-a_{q-1}) \times 10^{n-q}
$$
由于$(a_j,a_{n})$是一条递减序列,所以有:
$$
a_{k}\leq a_{j},a_{q-1}\leq a_{q-2},…,a_{q}\leq a_{q-1}
$$
即:
$$
a_{k}-a_{j}\leq 0,a_{q-1}-a_{q-2}\leq 0,a_{q}-a_{q-1}\leq 0
$$
所以有$T_{A’}-T_{A’’’}\leq 0$,那么$T_{A’}$是A删完$a_q(j< q \leq n)$后,所组成的最小数值。贪心选择是安全的。
综上(a)(b)所述,若A中只有两段单调子区间,且高位部分是递增子区间,低位部分是递减子区间,那么删去此递减子区间的首字符后,所组成的数是最小数值。贪心选择是安全的。
(2) 现在已经证明了如果A中只有一个山,那么删除山顶元素是最合适的。如果A中有多个山峰该如何处理?
换句话说,如果A中不止有2段单调子区间,而是由很多不同的单调子区间所组成,那应该如何处理?
这个问题看上去有点复杂了,我画个图吧:
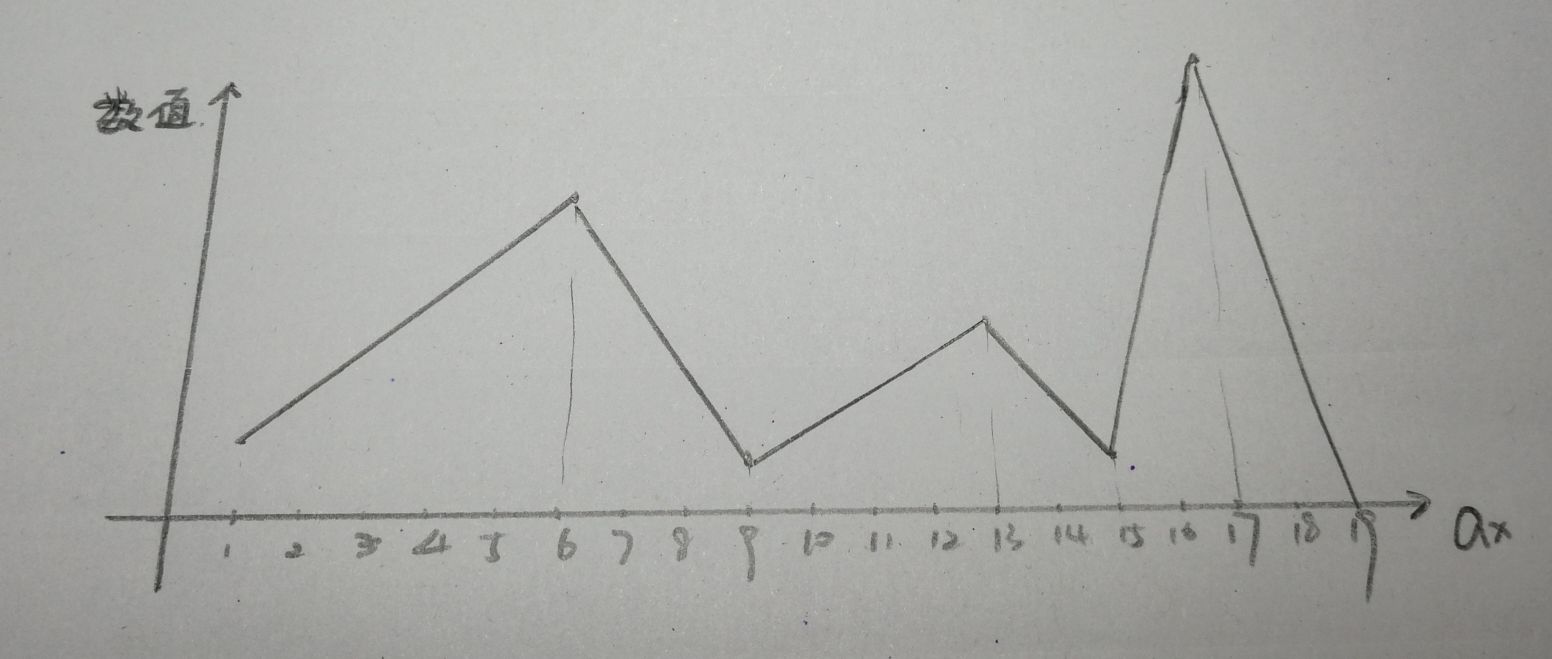
其实把图画出来后,我尝试着删除第一个山的山顶元素,删完后发现,现在的$a_6=a_5$,而$a_7=a_7$:
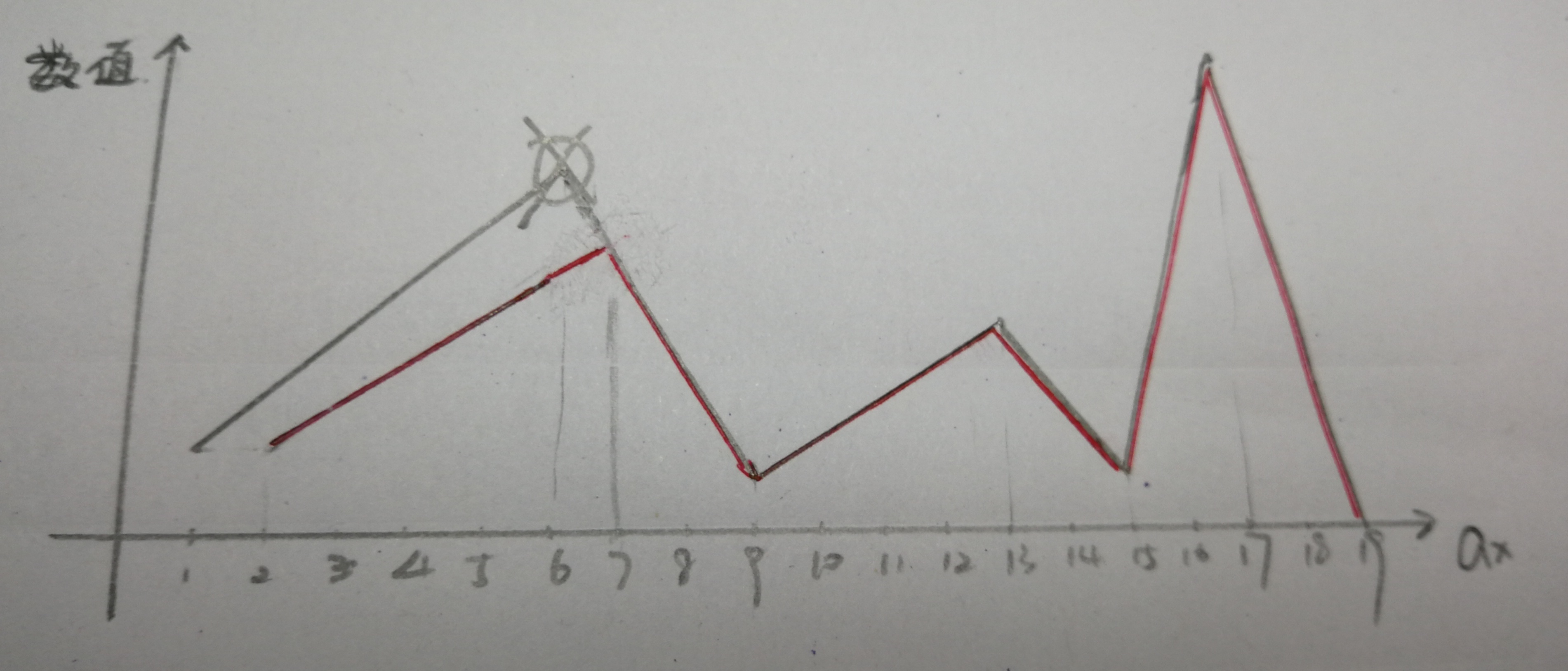
但如果删除第一个山之后的任意一个元素的话,删完后发现$a_6=a_5$,而现在的$a_7=a_6$。
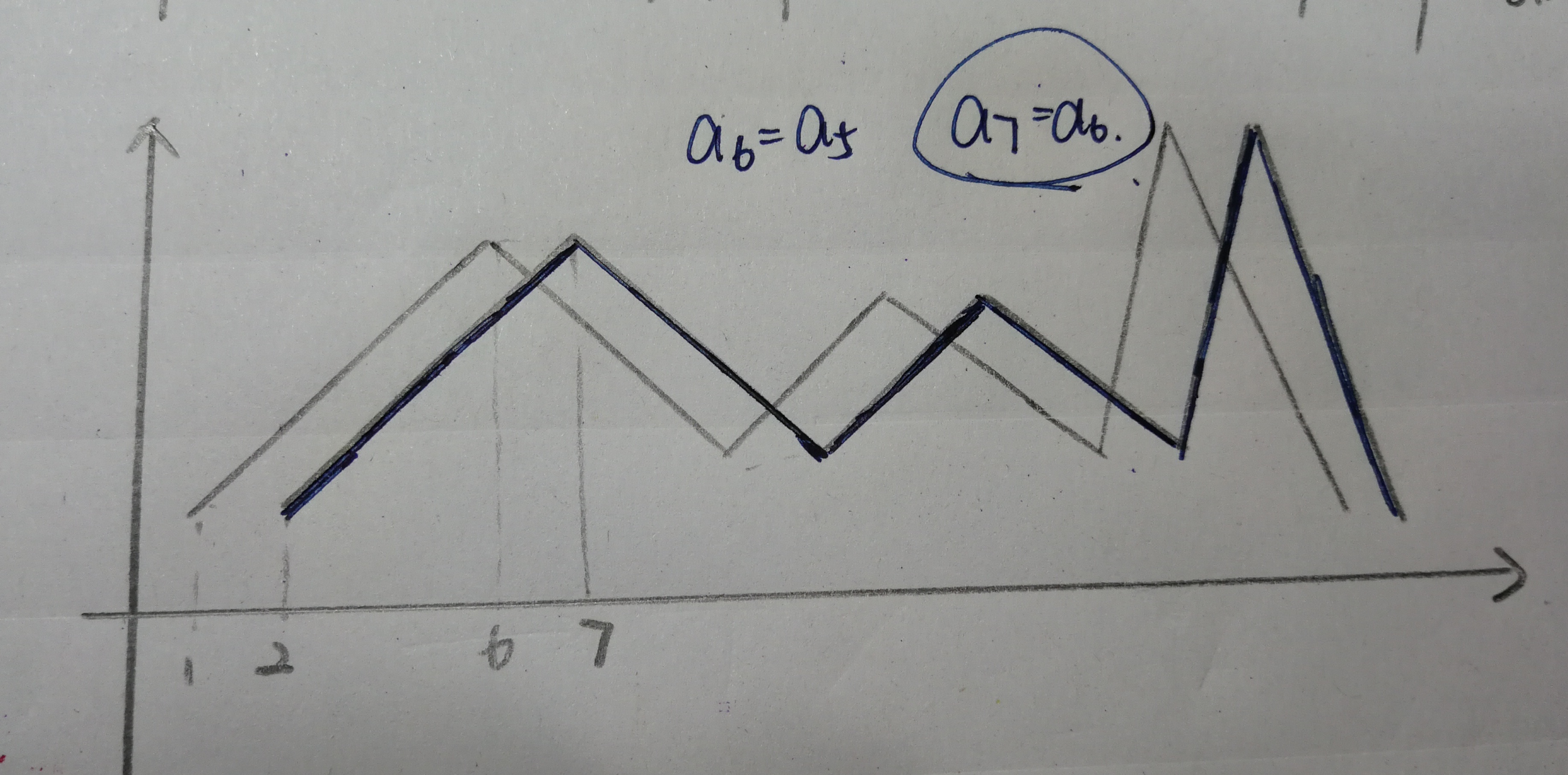
由于$a_6>a_7$,所以不管后面删哪个元素,都会比删除$a_6$所得到的数要大。
数学证明如下:
假设在A中,有3个连在一起的数$a_i,a_j,a_k(1\leq i< j< k\leq n)$,还有另一个数$a_r(k \leq r < n)$,,其中$(a_1,a_j)$是递增序列,$(a_j,a_r)$是递减序列。
记原本A所代表的数值为$T_A$,则有:
$$
T_A=a_1 \times 10^{n-1}+a_2 \times 10^{n-2}+…+a_i \times 10^{n-i}+a_j \times 10^{n-j}+a_k \times 10^{n-k}+…+a_{n-1} \times 10+a_n
$$
删除$a_j$后,A变为A’,A’所代表的数值为$T_{A’}$,则有:
$$
T_{A’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_i \times 10^{n-i-1}+a_k \times 10^{n-k}+…
$$
如果不删除$a_j$,而是删除另一个数$a_q(r \leq q \leq n)$。此时A变为A’’,A’’所代表的数值为$T_{A’’}$,则有:
$$
T_{A’’}=a_1 \times 10^{n-2}+a_2 \times 10^{n-3}+…+a_i \times 10^{n-i-1}+a_j \times 10^{n-j-1}+…
$$
发现$T_{A’}$中的$10^{n-k}$的系数是$a_k$,而$T_{A’’}$中的$10^{n-k}$的系数是$a_j$,由于$a_k< a_j$,那么必有$T_{A’}< T_{A’’}$,所以删除第一个山峰的峰值是安全的。也就是如果A[1…n]含有严格递减子序列,那么就删除第一个严格递减子序列的首字符。贪心选择是安全的。
综上,贪心选择性质成立。